Asymmetrische Verschlüsselung - Prof. Dr. Norbert Pohlmann
Asymmetrische Verschlüsselung | |
 | Inhaltsverzeichnis Was ist eine asymmetrische Verschlüsselung?
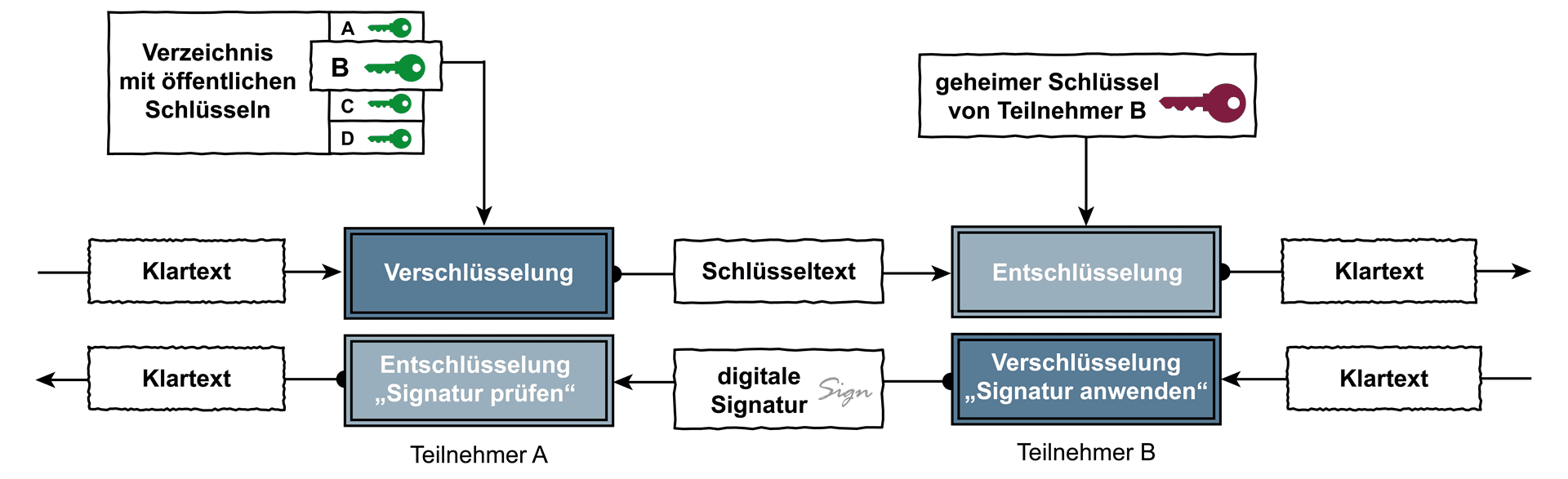
Dazu benötigt der Empfänger einen zweiten Schlüssel, den nur er allein kennt, den sogenannten Private Key oder geheimen Schlüssel. Damit dieses Verfahren auch wirklich sicher funktioniert, darf der geheime Schlüssel nicht aus dem öffentlichen Schlüssel ableitbar sein. Auch muss das Verfahren Angriffen mithilfe der Known-Plaintext– beziehungsweise Chosen-Plaintext-Methode widerstehen. Erfüllt das Public-Key-Verfahren beide Bedingungen, gibt es keinen Grund mehr, den Schlüssel für die Verschlüsselung geheim zu halten. Verfahren mit zwei unterschiedlichen Schlüsseln, die nicht voneinander ableitbar sind, werden als Public-Key-Verfahren gekennzeichnet. Der Schlüssel zur Verschlüsselung wird als öffentlicher Schlüssel bezeichnet und der Schlüssel zur Entschlüsselung privater oder geheimer Schlüssel genannt. Will Alice (A) eine vertrauliche Nachricht an Bob (B) senden, so entnimmt sie den öffentlichen Schlüssel von B einem Verzeichnis mit öffentlichen Schlüsseln, verschlüsselt den Klartext damit und sendet diesen als Schlüsseltext an B. Da nur B den zugehörigen geheimen Schlüssel kennt, und da dieser Schlüssel weder aus dem öffentlichen Schlüssel noch aus der verschlüsselten Nachricht, dem Schlüsseltext, bestimmt werden kann, ist B tatsächlich der Einzige, der den Schlüsseltext wieder zum Klartext entschlüsseln kann. Damit ist also eine sichere Kommunikation möglich, ohne dass dazu vorher eine geheime Schlüsselübermittlung zwischen A und B oder von dritter Seite an beide notwendig wäre.  Einwegfunktionen mit ParameterBeide Bedingungen – der geheime Schlüssel darf nicht aus dem öffentlichen Schlüssel ableitbar sein und das Verfahren muss der Chosen-Plaintext-Methode widerstehen – sind allerdings nicht so einfach einzuhalten. Das liegt zum einen daran, dass der geheime Schlüssel vom Prinzip her immer aus dem öffentlichen Schlüssel ableitbar ist, da zwischen beiden eine mathematische Relation besteht. Daher werden für Public-Key-Verfahren Algorithmen gewählt, die auf der Lösung von schweren Problemen der Komplexitätstheorie beruhen. Idealerweise handelt es sich um Funktionen, bei denen die Verschlüsselung „leicht“ zu berechnen, aber die Entschlüsselung ohne den geheimen Schlüssel unendlich komplex, das heißt praktisch „unmöglich“ ist. Die Begriffe „leicht“ und „unmöglich“ sollen den rechnerischen Aufwand beschreiben und hängen somit vom Entwicklungsstand der jeweiligen Computergeneration ab. Ein einfaches Beispiel hierfür ist die Primzahlenzerlegung. Es ist leicht, die Primzahlen 1237 und 2251 zu multiplizieren. Hingegen ist die Frage: „Welche beiden Primzahlen ergeben multipliziert die Zahl 2.100.457?“ deutlich schwerer zu bestimmen. Grundlegend basiert die Sicherheit des bereits genannten RSA-Verfahrens auf dieser Fragestellung. Die beiden Primzahlen sind 1627 und 1291. Die Lösung von schweren Problemen der Komplexitätstheorie ist zum Beispiel bei Exponentialfunktionen und diskreten Logarithmen oder dem Problem der Faktorisierung von Produkten zweier großer Primzahlen der Fall. Derartige Funktionen werden auch als One-Way- oder Einwegfunktionen bezeichnet. Die dabei eingesetzten Schlüssel sind insgesamt deutlich länger als bei symmetrischen Verschlüsselungsverfahren. Ein besonderer Fall ist gegeben, wenn für die benutzte Einwegfunktion ein Parameter beziehungsweise Schlüssel existiert, mit dem sich die inverse Transformation „leicht“ berechnen lässt. Derartige Funktionen werden one-way trap door functions (Einwegfunktionen mit Falltür oder Hintertür) genannt. Wie der geheime Schlüssel darf auch die „Hintertür“ ausschließlich dem legitimen Nutzer bekannt sein. Als Analogie kann ein Schnapp-Schloss betrachtet werden, jeder kann die Tür zu schlagen, aber derjenige, der den passenden Schlüssel hat, kann die Tür wieder aufschließen. 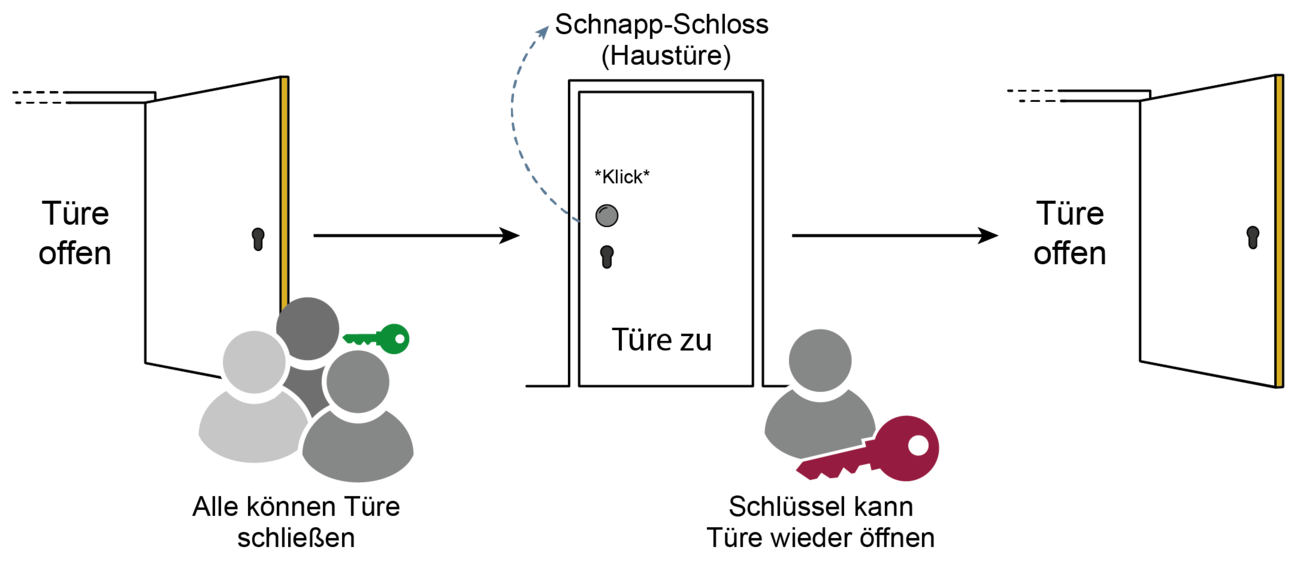 Beispiele von asymmetrische Verfahren:Weitere Informationen zum Begriff “Asymmetrische Verschlüsselung”:
„Übungsaufgaben und Ergebnisse zum Lehrbuch Cyber-Sicherheit“ „Bücher im Bereich Cyber-Sicherheit und IT-Sicherheit zum kostenlosen Download“
„Master-Studiengang Internet-Sicherheit (IT-Sicherheit, Cyber-Sicherheit)“ „Marktplatz IT-Sicherheit: IT-Notfall“ „Marktplatz IT-Sicherheit: IT-Sicherheitstools“ „Marktplatz IT-Sicherheit: Selbstlernangebot“ „Marktplatz IT-Sicherheit: Köpfe der IT-Sicherheit“ „Vertrauenswürdigkeits-Plattform“ Zurück zur Übersicht Summary  Article Name Asymmetrische Verschlüsselung Description Asymmetrische Verschlüsselung oder Public-Key-Verfahren sollen helfen, die Schlüsselverteilung und die digitale Signatur umzusetzen. Das wichtigste Kennzeichen ist, dass die Kommunikationspartner dabei, anstelle eines einzelnen geheimen Schlüssels, zwei verschiedene, aber trotzdem zusammengehörige Schlüssel nutzen. Author Prof. Norbert Pohlmann Publisher Name Institut für Internet-Sicherheit – if(is) Publisher Logo  |
 | |