RSA-Verfahren - Prof. Dr. Norbert Pohlmann
RSA-Verfahren | |
 | Inhaltsverzeichnis Was ist das RSA-Verfahren?
Werden die Faktoren dagegen hinreichend groß gewählt, kann die Zerlegung eine praktisch unlösbare Aufgabe darstellen. Das bedeutet, dass das Verfahren für einen definierten Zeitraum als „sicher“ gelten kann. Kryptografie-Experten empfehlen derzeit eine Länge von mindestent 3.000 Bit in binärer Darstellung für den RSA-Modulus. RSA-SchlüsselgenerierungUm einen Schlüssel nach RSA zu erzeugen, wird zunächst nach zwei großen Primzahlen p und q gesucht. Dann wird das Produkt n = p * q berechnet. Als nächstes wird eine zu ((p − 1) * (q − 1)) teilerfremde Zahl e ausgewählt. Diese bildet mit dem Produkt n den öffentlichen Schlüssel (e, n). Dann wird der erweiterte Euklidische Algorithmus verwendet, um eine Zahl d zu berechnen, wobei e * d mod ((p − 1) (q − 1)) = 1 gilt. Die Zahl d ist der geheime Schlüssel, der es ermöglicht, die Trap-Door-Eigenschaften des Verfahrens auszunutzen. Die Qualität des so erstellten Schlüssels und damit die Sicherheit des RSA-Verfahrens hängen von den verwendeten Primzahlen ab. RSA-VerschlüsselungsvorschriftEine Klartextnachricht m soll in einen Schlüsseltext c durch Verschlüsselung umgewandelt werden. Aus der Schlüsselgenerierung steht der öffentlichen Schlüssel (e, n) zur Verfügung, bestehend aus der zu ((p − 1) * (q − 1)) teilerfremden Zahl und dem Produkt der Primzahlen n. Außerdem steht der geheime Schlüssel d zur Verfügung.
c = me mod n.
m = cd mod n
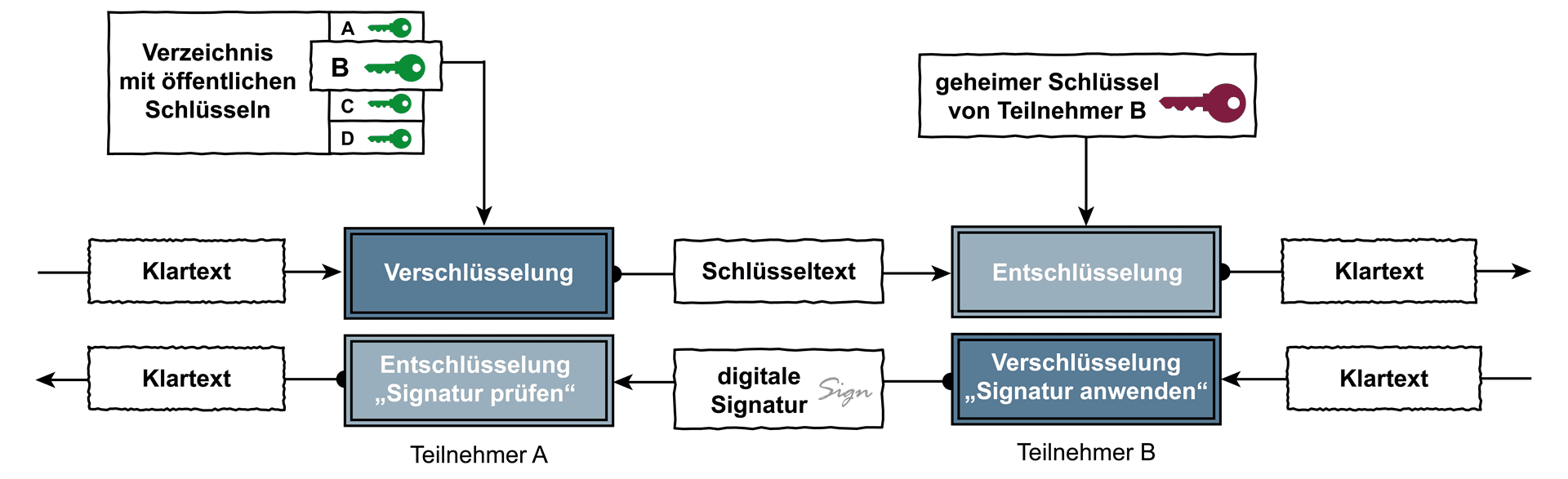
Beispiel RSA-Verschlüsselungp = 61 erste Primzahl Aufgabe 1 Aufgabe 2 Digitale Signatur mithilfe des RSA-VerfahrensEine wichtige Anwendung des RSA-Verfahrens ist die digitale Signatur. Sie nutzt beide Komponenten – sowohl den öffentlichen als auch den geheimen Schlüssel –, um mit ihrer Hilfe ein elektronisches Äquivalent zur eigenhändigen Unterschrift zu erzeugen, das ebenso rechtsverbindlich und im juristischen Sinn beweiskräftig ist wie eine eigenhändige Unterschrift. Klartext-Daten, die mit einem bestimmten geheimen Schlüssel „verschlüsselt“ wurden, können nur mithilfe des dazugehörigen öffentlichen Schlüssels wieder „entschlüsselt“ werden. Hat nun eine Person die Klartext-Daten mit ihrem geheimen Schlüssel digital signiert, kann mithilfe des öffentlichen Schlüssels überprüft werden, ob die digitale Signatur der Klartext-Daten wirklich von dieser Person stammt. Die erfolgreich durchgeführte Überprüfung der digitalen Signatur ist der Beweis für die Authentizität des Absenders und Integrität der Nachricht, dem Klartext. Mit dem Prinzip der digitalen Signatur steht somit ein Äquivalent zur eigenhändigen Unterschrift zur Verfügung. Das bekannteste Public-Key-Verfahren, mit dem gleichzeitig signiert und verschlüsselt werden kann, ist der RSA-Algorithmus. Authentische RSA-SchlüsselEin offenes Problem bei Public-Key-Verfahren wie dem RSA-Verfahren ist die Frage, wie der öffentliche Schlüssel zum Kommunikationspartner gelangt. Wie kann überprüft werden, dass ein öffentlicher Schlüssel in einem Verzeichnis wirklich der echte ist? Selbst im Fall der Verwendung öffentlicher Schlüssel müssen diese authentisch ausgetauscht werden. Siehe die Abbildung. Eine elegante Möglichkeit, öffentliche Schlüssel authentisch auszutauschen, ist die Einrichtung eines Zertifizierungssystems, eines Trustcenters oder einer Public-Key-Infrastruktur. Der öffentliche Schlüssel jedes Nutzers wird von einer Public-Key-Infrastruktur (Zertifizierungssystem) in Form eines „digitalen Zertifikate“ zur Verfügung gestellt. Schlussbetrachtung und Herausforderungen des RSA-VerfahrensAsymmetrische Verschlüsselungsverfahren sind im Vergleich zu symmetrischen Verschlüsselungsverfahren leider sehr rechenintensiv, weswegen die Ver- und Entschlüsselung deutlich langsamer vor sich geht. Die verwendeten Algorithmen müssen daher mit Blick auf Rechenleistung und Speicherplatz des verwendeten IT-Systems sowie die zur Verfügung stehende Zeit angepasst werden, um eine effektive Lösung zu realisieren.  Weitere Informationen zum Begriff “RSA-Verfahren”:
„Übungsaufgaben und Ergebnisse zum Lehrbuch Cyber-Sicherheit“ „Bücher im Bereich Cyber-Sicherheit und IT-Sicherheit zum kostenlosen Download“
„Blockchain-Technologie als Tool für Industrial Security“ „The Future of Trust in Ecosystems – Global Challenges“
„Master-Studiengang Internet-Sicherheit (IT-Sicherheit, Cyber-Sicherheit)“ Zurück zur Übersicht Summary  Article Name RSA-Verfahren Description Das RSA-Verfahren wurde 1978 entwickelt und findet seine Verwendung bei Verschlüsselung, digitalen Signaturen und beim Key Management. Der Algorithmus basiert auf dem Problem, dass das Produkt zweier großer Primzahlen nur schwer in seine Faktoren zu zerlegen ist. Author Prof. Norbert Pohlmann Publisher Name Institut für Internet-Sicherheit – if(is) Publisher Logo  |
 | |