Diffie-Hellman-Verfahren - Prof. Dr. Norbert Pohlmann

Was ist das Diffie-Hellman-Verfahren?

Das Diffie-Hellman-Verfahren (kurz DH) war der erste Public-Key-Algorithmus und wurde 1976 vorgestellt. Das Verfahren dient jedoch nicht der Verschlüsselung, sondern wurde entwickelt, um geheime Schlüssel (Diffie-Hellman Shared Secret) gesichert über einen unsicheren Kommunikationskanal auszutauschen. Dazu bedienten sich die Autoren Whitfield Diffie und Martin E. Hellman des Problems der diskreten Logarithmen.

Die Funktioneweise vom Diffie-Hellman-Verfahren

Das Schlüsselpaar des Kommunikationspartners A besteht aus einem geheimem Schlüssel prv_A und einem öffentlichen Schlüssel pub_A. pub_A errechnet sich aus dem geheimen Schlüssel pub_A mittels der Formel:

pub_A = g^prvA mod n

Jeweils öffentlich bekannt für alle Kommunikationspartner sind g und n, wobei n eine lange Primzahl ist und g eine zu n teilerfremde Zufallszahl.
Der Kommunikationspartner B errechnet analog sein Schlüsselpaar mit dem geheimen Schlüssel prv_B und dem öffentlichen Schlüssel pub_B. Die Zahlen prv_A und prv_B sind jeweils Zufallszahlen. Ziel des Diffie-Hellman-Verfahrens ist die Vereinbarung eines geheimen Schlüssels S (Diffie-Hellman Shared Secret), ohne dass zuvor Parameter zwischen den Kommunikationspartnern ausgetauscht werden müssen.

Ablauf des Diffie-Hellman-Verfahrens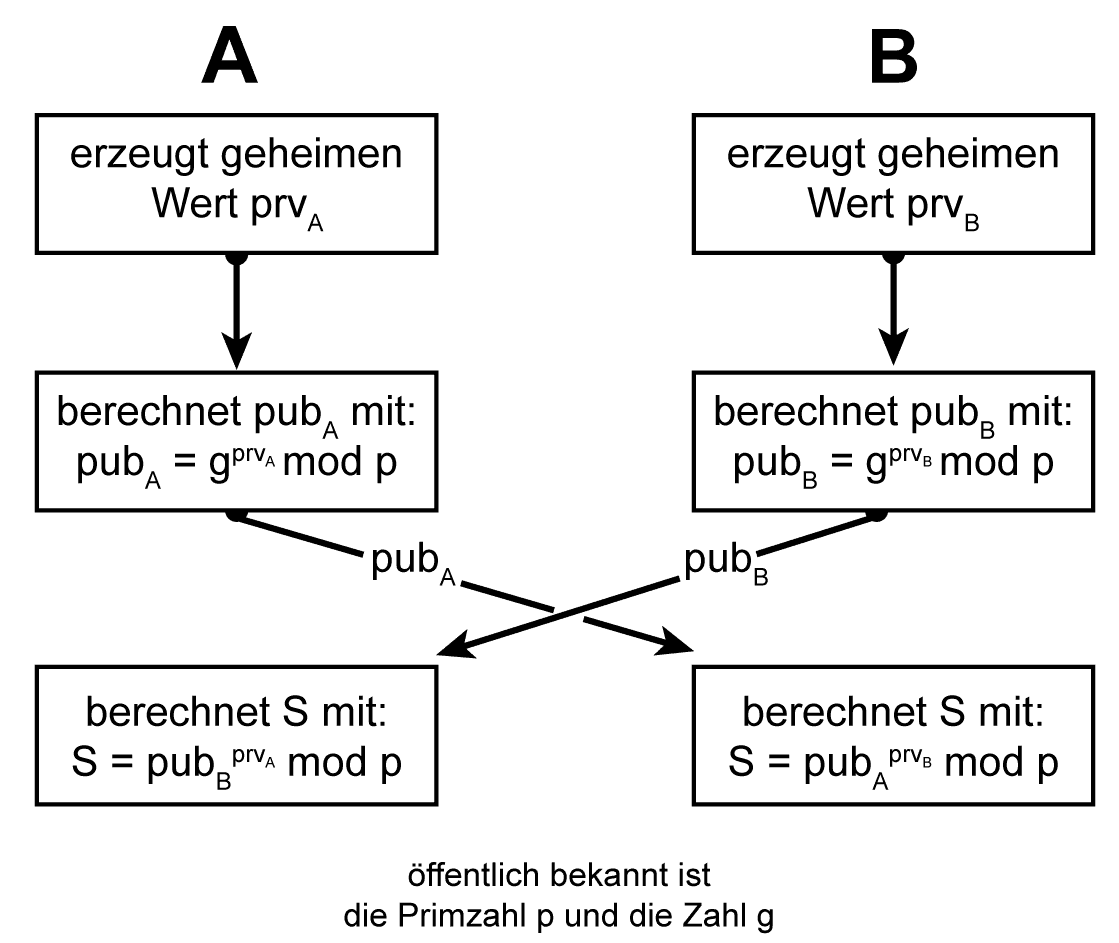

Die Kommunikationspartner berechnen nun jeweils ihren öffentlichen Schlüssel nach der vorgestellten Formel und schicken diesen an den Partner.
Der gemeinsame Schlüssel S (Diffie-Hellman Shared Secret) errechnet sich dann als

S = pub_B^prvA mod p

für Kommunikationspartner A und

S = pub_A^prvB mod p

für Kommunikationspartner B.

Dabei ist das errechnete S (geheimer Schlüssel – Diffie-Hellman Shared Secret) jeweils identisch. Eingesetzt wird das Diffie-Hellman-Verfahren unter anderem bei SSL/TLS und IPSec.

Auf den ersten Blick scheinen damit alle Schlüsselaustauschprobleme beseitigt.
Bei näherer Betrachtung wird allerdings klar, dass auch das Diffie-Hellman-Verfahren eine Schwachstelle hat: Eine Authentifizierung der Kommunikationspartner untereinander wird nicht realisiert, was die Methode anfällig für einen sogenannten Man-in-the-Middle-Angriff macht. Bei dieser Attacke leitet der Angreifer den gesamten Kommunikationsvorgang über sein eigenes IT-System um und sitzt so quasi zwischen seinen Opfern. Der eigentlich zwischen A und B auszuhandelnde Schlüssel S wird also tatsächlich jeweils zwischen den Opfern und dem Angreifer ausgehandelt. Die Authentifikation der Kommunikationspartner muss beim Diffie-Hellman-Verfahren mithilfe weiterer Verfahren, z. B. das RSA-Verfahren, umgesetzt werden.

Das Diffie-Hellman-Verfahren ist kein Verschlüsselungsalgorithmus und es gewährleistet auch keine Authentifizierung der Kommunikationspartner. Es dient dem gesicherten Austausch eines geheimen Schlüssels S über einen unsicheren Kommunikationskanal.

Beispiel: Der Handshake zum Verbindungsaufbau mit TLS 1.3

Bei TLS 1.3. wird im ersten Schritt neben anderen Informationen vom Client A der “Diffie Hellmann (DH) Public Key A” gesendet. Im Schritt 2 sendet der Server B neben weiteren Informationen seinen “Diffie Hellmann (DH) Public Key B”. Damit sind beide Seiten – Client A und Server B – in der Lage, den Sitzungsschlüssel zu berechnen.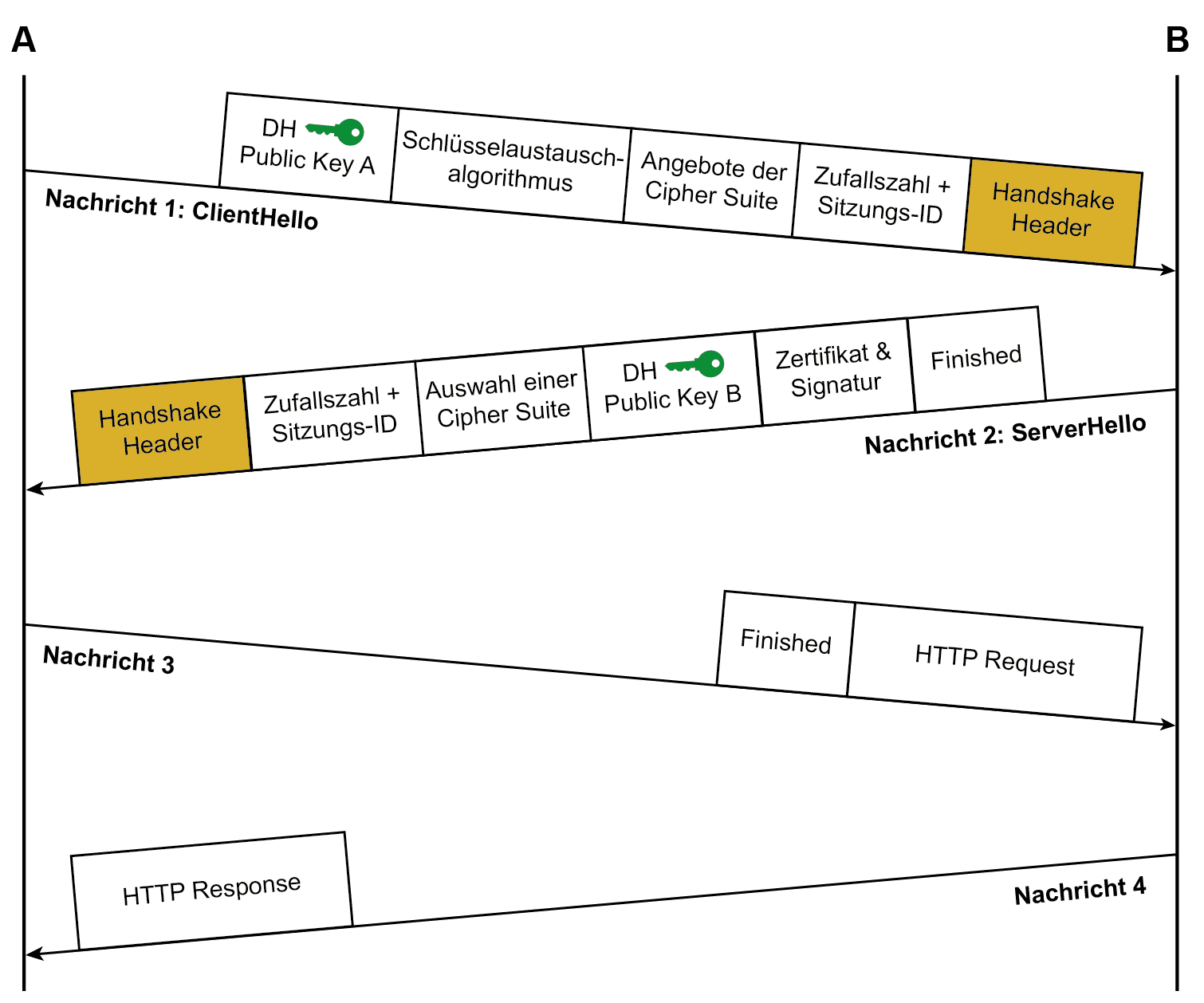

Die Authentifikation bei TLS wird auf der Basis der Zertifikate umgesetzt. Siehe TLS
Das Diffie-Hellman-Verfahren wird für die Umsetzung von Perfect Forward Secrecy (PFS) verwendet, weil dabei der Sitzungsschlüssel nicht übertragen werden muss.

Weitere Informationen zum Begriff “Diffie-Hellman-Verfahren”:

„Kryptographie: Von der Geheimwissenschaft zur alltäglichen Nutzanwendung“
– Elementare Verschlüsselungsverfahren
– Symmetrische Verschlüsselungsverfahren
– Asymmetrische Verschlüsselungsverfahren
– Prüfsummen, Zertifikate und die elektronische Signatur
– Public Key Infrastruktur (PKI)
– Vertrauensmodelle von Public-Key-Infrastrukturen

„Lehrbuch Cyber-Sicherheit“

„Übungsaufgaben und Ergebnisse zum Lehrbuch Cyber-Sicherheit“

„Bücher im Bereich Cyber-Sicherheit und IT-Sicherheit zum kostenlosen Download“

„Vorlesungen zum Lehrbuch Cyber-Sicherheit“

„Cyber-Sicherheitsstrategien zur Reduzierung der Risiken für Unternehmen“

„Cloud security made for the EU: Securing data and applications“

„Internet Security Survey 2023“

„Immer mehr Daten = Immer mehr (Un) Sicherheit?“

„Forschungsinstitut für Internet-Sicherheit (IT-Sicherheit, Cyber-Sicherheit)“

„Master-Studiengang Internet-Sicherheit (IT-Sicherheit, Cyber-Sicherheit)“

„Marktplatz IT-Sicherheit“

„Marktplatz IT-Sicherheit: IT-Notfall“

„Marktplatz IT-Sicherheit: IT-Sicherheitstools“

„Marktplatz IT-Sicherheit: Selbstlernangebot“

„Marktplatz IT-Sicherheit: Köpfe der IT-Sicherheit“

„Vertrauenswürdigkeits-Plattform“

Summary

Article Name

Diffie-Hellman-Verfahren

Description

Mithilfe des Diffie-Hellman-Verfahrens können geheime Schlüssel gesichert über einen unsicheren Kommunikationskanal auszutauschen werden. Es wurde 1976 als erste Public-Key-Algorithmus vorgestellt und bedient sich des Problems der diskreten Logarithmen.

Author

Prof. Norbert Pohlmann

Publisher Name

Institut für Internet-Sicherheit – if(is)

Publisher Logo